설치링크
무료 회로설계 툴 LTspice 최신버전 다운로드, 단축키, 튜토리얼, 화면 확대 스크롤 방향 변경
LTspice 설치 링크 https://www.analog.com/en/lp/002/tools/ltspice-simulator-kr.html LTspice | Analog Devices www.analog.com LTspice 단축키 W wire G ground V voltage C capacitor R resistor L inductor D diode ctrl + R 회전 Backspace 지우기 N netna
semi52.tistory.com
지난 글
짱쉬운 LTspice 강의 3강 - RC 직렬, 병렬 전자회로 시뮬레이션 / 양단 전압 전류 측정 방법
설치링크 무료 회로설계 툴 LTspice 최신버전 다운로드, 단축키, 튜토리얼, 화면 확대 스크롤 방향 변경 LTspice 설치 링크 https://www.analog.com/en/lp/002/tools/ltspice-simulator-kr.html LTspice | Analog Devices www.analo
semi52.tistory.com
오늘은 RLC 회로 실습을 해볼게요.
먼저 이글은 아래 블로거 님의 이론, 실습 과정을 참고해 쓴 글입니다.
이론 링크는 아래 글을 참고해 주시고요.
[전자 회로 실험] #2-(1). RLC 회로 설계하기 (RLC 필터)
본 실험에서는 직렬 RLC 회로를 설계해보고 RLC 회로에서 Overdamping과 Underdamping이 되는 조건을 알아보겠습니다. 또한, 직렬 RLC 회로의 전달함수를 구하고 전달함수의 주파수에 따른 위상과 크기 특
ing-s.tistory.com
먼저 필터란 뭘까요?
인덕터는 교류 회로의 주파수가 낮을수록 전류를 잘 통과시키고, 커패시터는 교류 회로의 주파수가 높을수록 전류를 잘 통과시켜요.
이러한 주파수 특성때문에, 인덕터와 커패시터는 전기신호의 원하는 주파수를 걸러내거나 원하지 않는 주파수의 전류를 막는 역할을 할 수 있어요.
저역통과 필터 (Low-pass filter: LPF)
낮은 주파수는 통과시키고, 높은 주파수는 저지시킵니다.

고역통과 필터 (High-pass filter: HPF)
높은 주파수는 통과시키고, 낮은 주파수는 저지시킵니다.

이번 실험에서 가장 중요한 사진이에요.


위와 같이 저항, 인덕터, 커패시터로 이루어진 회로를 RLC 회로라고 해요.
위 회로에 각 소자에 걸리는 전압, 전류를 KVL을 이용해 미분방정식을 세워볼게요.
$$ -V+L\frac{di}{dt}+iR+\frac{1}{C}\int idt=0$$
양변을 시간에 대해서 미분하면
$$L\frac{d^2i}{dt^2}+R\frac{di}{dt}+\frac{1}{C}i=0$$
미분방정식을 특성방정식의 꼴로 바꾸면
$$s^2+2\alpha s+\omega _0^2 = 0$$
$$\alpha = \frac{R}{2L}$$
$$\omega _0 = \frac{1}{\sqrt{LC}}$$
여기서 $\alpha$는 감쇠지수, $\omega _0$는 고유 진동수를 나타내요
이때 $\alpha$와 $\omega _0$ 에 따라 해가 달라지게 돼요.
감쇠계수 $\alpha$가 공진 주파수 $\omega _0$ 보다 작을 경우에 Underdamped
감쇠계수 $\alpha$와 공진 주파수 $\omega _0$ 가 같을 경우에 Critically Damped
감쇠계수 $\alpha$가 공진 주파수 $\omega _0$ 보다 클 경우에 Overdamped
실습과정은 아래에 있어요.
[전자 회로 실험] #2-(2). RLC 회로 설계하기 (RLC 필터)
RLC 회로 설계에 대한 배경 지식은 이전의 포스팅을 참고해주시기 바랍니다. [회로 설계/전자 회로 설계] - [전자 회로 실험] #2-(1). RLC 회로 설계하기 (RLC 필터) 사전 실험 앞서 설명한 실험에 대한
ing-s.tistory.com
위 글에서 실습과정은 pspice로 이루어졌는데 저는 ltspice를 사용해서 실습을 해볼게요.
감쇠계수 $\alpha$가 공진 주파수 $\omega _0$ 보다 작을 경우에 Underdamped
$$\alpha = \frac{R}{2L}$$
$$\omega _0 = \frac{1}{\sqrt{LC}}$$
$$감쇠계수 \,\alpha\, <\, 공진 주파수\, \omega _0 \, 이니까\,위\,값을 \, 대입하면 $$
$$\frac{R}{2L} \,<\, \frac{1}{\sqrt{LC}} 이고 \, 양변에\, \sqrt{LC} \, 을 \, 곱하면 $$
$$\frac{R}{2}\sqrt{\frac{C}{L}}\, <\, 1$$
이를 만족하도록 소자의 값을 R = 5k[Ohm], L = 100mH, C = 1nF 으로 설정하여 Simulation 해준 결과는 다음과 같아요.
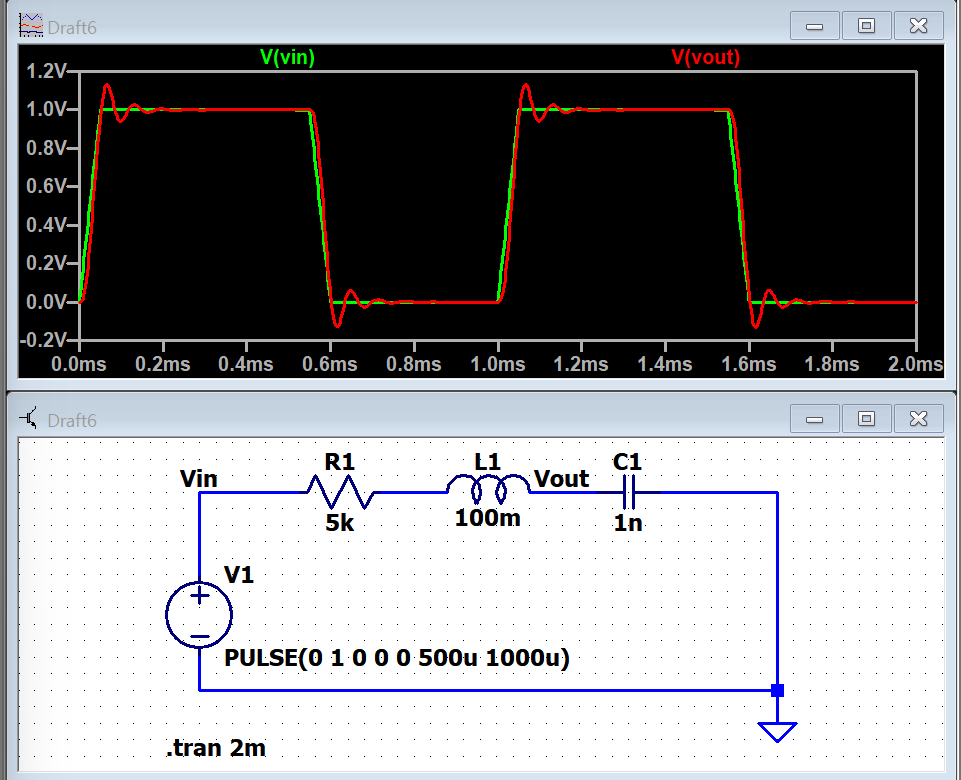
감쇠계수 $\alpha$가 공진 주파수 $\omega _0$ 보다 클 경우에 Overdamped
$$\frac{R}{2}\sqrt{\frac{C}{L}}\, >\, 1$$
위의 조건에 맞게 R = 30k[Ohm], L = 100mH, C = 1nF 으로 설정을 하여 Simulation

감쇠계수 $\alpha$와 공진 주파수 $\omega _0$ 가 같을 경우에 Critically Damped
아래 링크에 가면 실시간으로 직접 실습해볼 수도 있어요.
참고자료
[전자 회로 실험] #2-(2). RLC 회로 설계하기 (RLC 필터)
RLC 회로 설계에 대한 배경 지식은 이전의 포스팅을 참고해주시기 바랍니다. [회로 설계/전자 회로 설계] - [전자 회로 실험] #2-(1). RLC 회로 설계하기 (RLC 필터) 사전 실험 앞서 설명한 실험에 대한
ing-s.tistory.com
LC 필터 - 자바실험실
인덕터는 교류 회로의 주파수가 낮을수록 전류를 잘 통과시키고, 커패시터는 교류 회로의 주파수가 높을수록 전류를 잘 통과시킵니다. 이러한 주파수 특성때문에, 인덕터와 커패시터는 전기신
javalab.org
RLC 직렬 회로 - 자바실험실
RLC 직렬 회로 저항(R)-인덕터(L, 코일)-커패시터(C, 축전기)가 직렬로 연결된 회로를 생각해 봅시다. 매순간 회로에 흐르는 전류는 회로의 어디서나 같습니다. (매우 중요하니, 꼭 기억해 둡시다.)
javalab.org
이어지는 글
짱쉬운 LTspice 강의 5강 - IV 커브 그리기, 가변 소자값 시뮬레이션
설치링크 무료 회로설계 툴 LTspice 최신버전 다운로드, 단축키, 튜토리얼, 화면 확대 스크롤 방향 변경 LTspice 설치 링크 https://www.analog.com/en/lp/002/tools/ltspice-simulator-kr.html LTspice | Analog Devices www.analo
semi52.tistory.com
[세미피디아] 집적회로설계란? Integrated circuit design
https://en.wikipedia.org/wiki/Integrated_circuit_design 집적 회로 설계, 반도체 설계, 칩 설계 또는 IC 설계는 전자 공학의 하위 분야로, 집적 회로 또는 IC를 설계하기 위해 필요한 특정 로직과 회로 설계 기법
semi52.tistory.com
'반도체 > 회로설계' 카테고리의 다른 글
| 😎짱쉬운 LTspice 강의 6강 - LTspice로 반파정류기, 제너다이오드, 전파정류기 구현하기 (1) | 2024.03.25 |
|---|---|
| 😎짱쉬운 LTspice 강의 5강 - IV 커브 그리기, 가변 소자값 시뮬레이션 (1) | 2024.03.25 |
| RF 회로개념 - Filter 참고링크 (0) | 2024.03.24 |
| 😎짱쉬운 LTspice 강의 3강 - RC 직렬, 병렬 전자회로 시뮬레이션 / 양단 전압 전류 측정 방법 (2) | 2024.03.23 |
| 😎짱쉬운 LTspice 강의 2강 - pulse파의 이해와 RC회로 충방전 전자회로 실습 (0) | 2024.03.23 |

